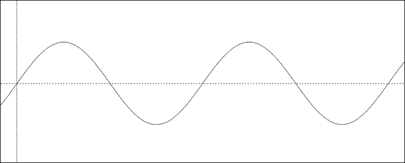
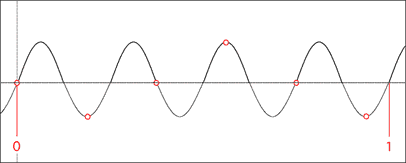
Digital Audio Sampling 1

One of the most basic sounds that we can produce is called a sine wave. It is called this because the pattern is based of the trigonometric function of the same name. It looks like this:

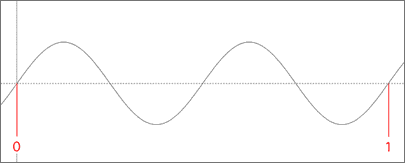
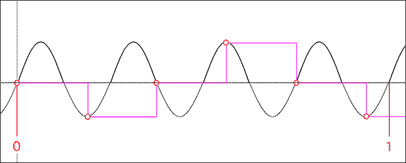
The y-axis on this graph represents the positive and negative fluctuations in air pressure that create sound. The center line represents a position of rest. If a graph were to remain on this line, it would mean that there were no changes and the sound would be silent. More on that in the next tutorial.

The x-axis represents time which increases from left to right. If there is a repeating pattern seen on the x-axis, then the sound is likely pitched. The number of repetitions is measured in Hertz (Hz), or cycles per second. Since the following graph is marked at the zero and one second mark...

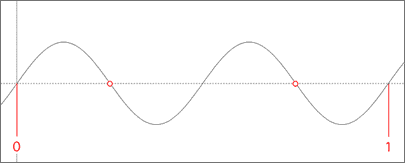
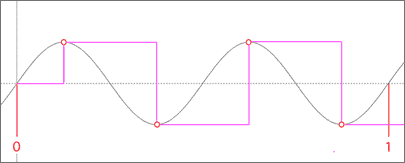
...we can see that the pattern repeats twice within that second. The sine wave would therefore be called a 2 Hertz sine wave.

In a digital audio system, the sound wave is sampled a specific number of times within each second. The playback system uses these samples to reconstruct the waveform. How well it is able to do this is dependent on several factors.

One factor is how many times the waveform is sampled per second. This is called the sampling rate and is also measured in Hertz. No information is recorded between samples, so if you do not use a high enough sampling rate you could end up not recording all of the changes present in the sound. Of course, the trade off is that the higher the sampling rate is, the more memory your digital recording will use, leading to larger file sizes.

If you were to use a sampling rate of 2 Hz on the waveform we are currently discussing, it might look something like this...

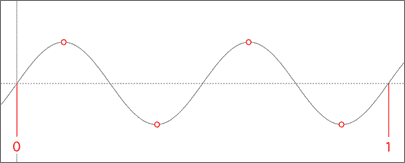
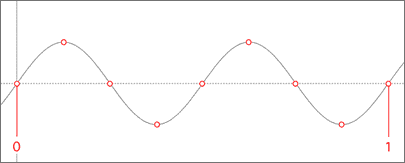
You should notice that the two samples have caught the waveform at the zero line. Based on this information, there is no way that the waveform can be reconstructed. If we increase the sampling rate to 4 Hz...

...you can see that we now have enough information to reconstruct the waveform like this...

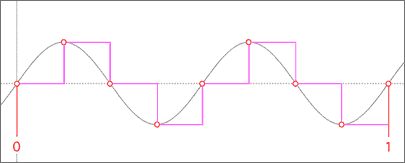
Of course, increasing the sampling rate to 8 Hz like this...

...we could recreate the waveform a bit better, like this...

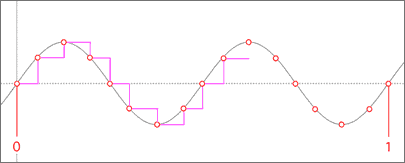
And using a sampling rate of 16 Hz would be even more accuracy...

You get the idea. Now this accuracy also has another effect known as aliasing. Aliasing occurs when a the sampling rate is not fast enough to capture a given frequency. If we wanted to record a 4 Hz sine wave but were only digitally recording the changes at about a 6 Hz sampling rate, it might look something like this...

When the digital playback system attempts to reconstruct the waveform, it might look like the following...

You can see that the digital reconstruction has fewer cycles than the actual waveform we attempted to record. We say that the frequency has aliased to the new, lower frequency. This is a problem, since we would obviously like to accurately record the sound for later playback. If we have frequencies that are aliasing, then the digital recording will not sound like the original.

The Nyquist theorem is a guideline meant to help prevent this problem from occurring. It states that you must use a sampling rate that is at least twice that of the highest frequency you would like to record. The highest frequency that a sampling rate is capable of recording is known as the Nyquist frequency. We can express the relationship between the Nyquist frequency and the sampling rate by saying...

FS = 2 * FN

If human hearing is capable of hearing frequencies as high as 20,000 Hz, what is the minimum sampling rate that we can use to record the range of audible frequencies? We can plug this number into our formula as a hypothetical Nyquist frequency and then solve it...

2 * 20,000 = 40,000

The answer of 40,000 samples per second is not that far off from CD quality sound. In fact, CDs offer a little bit higher rate due to some other issues that are a bit too complicated to go into right now. CDs have a sampling rate of 44,100 samples per second. It will often be referred to as 44.1 kilohertz (kHz), which simply uses the standard metric prefix "kilo" to mean "thousand".

The next tutorial will address the other half of digital sampling: the bit depth.